ブランコの計算

問題
軸に固定したひもの先に重りが付けてある。
ひもを張った状態で45度の角度まで重りを引き上げてから重りを自由運動させることにする。
重りはあるタイミングでひもから切り離せる仕組みになっている。
ここで、何度の角度の時に重りを切り離すと重りは一番遠くまでとばすことが出来るか答えよ。
また、ひもの長さが３ｍの時、飛ばすことが出来る最大長さを答えよ。
ひもの固定部分の抵抗やひもの重さ及び空気抵抗は無視する。


要はブランコ飛びの問題ですが、もうすっかり物理は忘れてしまいました。
テレビ番組でブランコに乗って海を飛び込む距離の競い合いを見てこの問題を思い出しましたが、
解答が考えられなくなっている自分に歳を感じちゃいましたよ。
どんな計算式だっただろう。解答を教えてくださらないか。
設問の細かい突っ込みは無しにしてね。

返信する

高さ書かなきゃだめじゃん

返信する

>2
ひもの頂点の高さは５ｍにしましょ　

返信する

数値計算したら、約24.6度のときで3.89mとなった。
計算自信なし。
どなたか賢い人が一般解を出してくれるでしょう。。。

返信する

重りにプロペラ付けていいんだっけ？

返信する

きのうの鉄腕ダッシュの影響だな

返信する

そうなんよ　昨日の鉄腕ダッシュを見ていてこんな問題有ったなって思い出したんだ。
>4さんの言うように一般解をどなたか解いてくれ。

返信する

削除（by投稿者）

返信する

９回裏同点の犠牲フライまでは打てるんだけど…

返信する

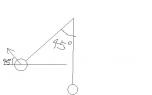
マジレスすると４５度のとき一番と置くまで飛ぶ。

返信する

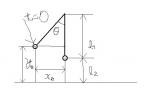
間違えた。
紐の長さを：L1、重りの高さを：L2、紐を切った位置を（Xθ、Yθ）、紐を切ったときの時刻をt＝0、切ったときの速度を：Vとするとだ

X＝Xθ＋VｔSINθ＝L1SINθ＋VtSINθ
Y＝Yθ−（ｇt^2）/2+VtCOSθ＝L2+L1(1−COSθ)−(gt^2)/2+vtCOSθ

ここでy=0となるときのtを求めると

ｔ=[ｖCOSθ±[V^2×COS^2θ＋4g{L2−L1(1−COSθ)}]^(1/2)]/2g

このｔをXの式の中のｔに当てはめてX最大となるようなθの値を求めるればいい
のだけど思ったよりかなり複雑になった。ペンタブもないしすらすらかけないよｗ

返信する

L1、L2が未知数なうえにⅩθ、Yθが影響するから
一概にθがいくつの時最大になるとはいえない。
こういうのは問題作る側にセンスが求められるよなｗ

飛び出すときのVはエネルギー保存則をつかえば出る。

返信する

アルプスの少女ハイジのブランコはどうなってんだ？？？

返信する

一般＆特殊相対性理論の影響を考慮しなければならない。

返信する

紐の長さと玉の質量を１とし、離れる瞬間の時間をt=0としても一般性は失われない。
振り子の中心の高さを 1+L とする。
重力加速度をgとおいて、それぞれ玉が離れる振れ角度,位置、速度をそれぞれ
theta,x_0,y_0,vx_0,vy_0とすると、
　x_0 = sin(theta)
　y_0 = 1+L-cos(theta)
　vx_0 = sqrt(2*g*(1/sqrt(2)-sin(theta))/(1+(tan(theta))^2))
vy_0 = vx_0^2 (tan(theta))^2
となるから,任意のthetaとtにおける玉の放物運動を完全に計算することができることが分かる。
着地するときの時間は
t_1 = (vy_0+sqrt(vy_0^2+2*g*(1+L-cos(theta))))
となり、そのときの距離は
x_1 = x_0 + vx_0*t_1
となり、x_1をthetaで微分すれば最大の距離になるthetaが導出できる。

ただL>>1の場合以外で、この微分を手で計算するのはすこぶる難しい。

返信する

アルプスの少女は

返信する

誰か早く解いてくれ
今、ハイパーオリンピックの幅跳びと槍投げでハイスコアを狙ってるんだ

返信する

.

返信する

削除（by投稿者）

返信する

アナル拡張師への哀歌

返信する

アナル拡張師への哀歌

返信する